How to Read a Radioactive Decay Graph
Nuclear Physics
75 Radioactive Decay
Learning Objectives
By the end of this section, you lot volition be able to:
- Draw the decay of a radioactive substance in terms of its decay constant and one-half-life
- Utilize the radioactive decay law to judge the age of a substance
- Explicate the natural processes that allow the dating of living tissue using
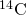
In 1896, Antoine Becquerel discovered that a uranium-rich rock emits invisible rays that can darken a photographic plate in an enclosed container. Scientists offer iii arguments for the nuclear origin of these rays. First, the effects of the radiation do non vary with chemical country; that is, whether the emitting material is in the form of an element or compound. Second, the radiation does not vary with changes in temperature or pressure—both factors that in sufficient degree can bear on electrons in an cantlet. 3rd, the very large free energy of the invisible rays (up to hundreds of eV) is not consistent with atomic electron transitions (only a few eV). Today, this radiation is explained by the conversion of mass into energy deep within the nucleus of an atom. The spontaneous emission of radiation from nuclei is called nuclear radioactivity ((Figure)).
The international ionizing radiation symbol is universally recognized equally the warning symbol for nuclear radiation.

Radioactive Disuse Constabulary
When an individual nucleus transforms into some other with the emission of radiation, the nucleus is said to decay. Radioactive decay occurs for all nuclei with ![]() and too for some unstable isotopes with
and too for some unstable isotopes with ![]() The decay rate is proportional to the number of original (undecayed) nuclei North in a substance. The number of nuclei lost to disuse,
The decay rate is proportional to the number of original (undecayed) nuclei North in a substance. The number of nuclei lost to disuse, ![]() in fourth dimension interval dt, is written
in fourth dimension interval dt, is written
![]()
where ![]() is called the disuse abiding. (The minus sign indicates the number of original nuclei decreases over time.) In other words, the more nuclei available to decay, the more than that do decay (in time dt). This equation tin be rewritten as
is called the disuse abiding. (The minus sign indicates the number of original nuclei decreases over time.) In other words, the more nuclei available to decay, the more than that do decay (in time dt). This equation tin be rewritten as
![]()
Integrating both sides of the equation, and defining ![]() to be the number of nuclei at
to be the number of nuclei at ![]() , we obtain
, we obtain
![]()
This gives united states
![]()
Taking the left and correct sides of the equation as a power of e, we have the radioactive decay police.
Radioactive Decay Law
The full number N of radioactive nuclei remaining afterward time t is
![]()
where ![]() is the decay constant for the particular nucleus.
is the decay constant for the particular nucleus.
The full number of nuclei drops very rapidly at first, then more slowly ((Figure)).
A plot of the radioactive decay law demonstrates that the number of nuclei remaining in a decay sample drops dramatically during the first moments of decay.

The half-life ![]() of a radioactive substance is defined as the time for half of the original nuclei to decay (or the time at which half of the original nuclei remain). The half-lives of unstable isotopes are shown in the chart of nuclides in (Figure). The number of radioactive nuclei remaining after an integer (n) number of half-lives is therefore
of a radioactive substance is defined as the time for half of the original nuclei to decay (or the time at which half of the original nuclei remain). The half-lives of unstable isotopes are shown in the chart of nuclides in (Figure). The number of radioactive nuclei remaining after an integer (n) number of half-lives is therefore
![]()
If the decay constant (![]() ) is large, the half-life is small, and vice versa. To determine the relationship betwixt these quantities, annotation that when
) is large, the half-life is small, and vice versa. To determine the relationship betwixt these quantities, annotation that when ![]() , and so
, and so ![]() . Thus, (Figure) can be rewritten every bit
. Thus, (Figure) can be rewritten every bit
![]()
Dividing both sides by ![]() and taking the natural logarithm yields
and taking the natural logarithm yields
![]()
which reduces to
![]()
Thus, if nosotros know the one-half-life T 1/two of a radioactive substance, we tin can find its disuse abiding. The lifetime ![]() of a radioactive substance is defined every bit the average amount of time that a nucleus exists before decaying. The lifetime of a substance is just the reciprocal of the decay constant, written as
of a radioactive substance is defined every bit the average amount of time that a nucleus exists before decaying. The lifetime of a substance is just the reciprocal of the decay constant, written as
![]()
The activity A is divers every bit the magnitude of the decay rate, or
![]()
The infinitesimal alter dN in the time interval dt is negative because the number of parent (undecayed) particles is decreasing, and then the activeness (A) is positive. Defining the initial activity as ![]() , we have
, we have
![]()
Thus, the activeness A of a radioactive substance decreases exponentially with time ((Figure)).
(a) A plot of the activeness as a office of fourth dimension (b) If we measure the action at different times, we tin plot ln A versus t, and obtain a directly line.
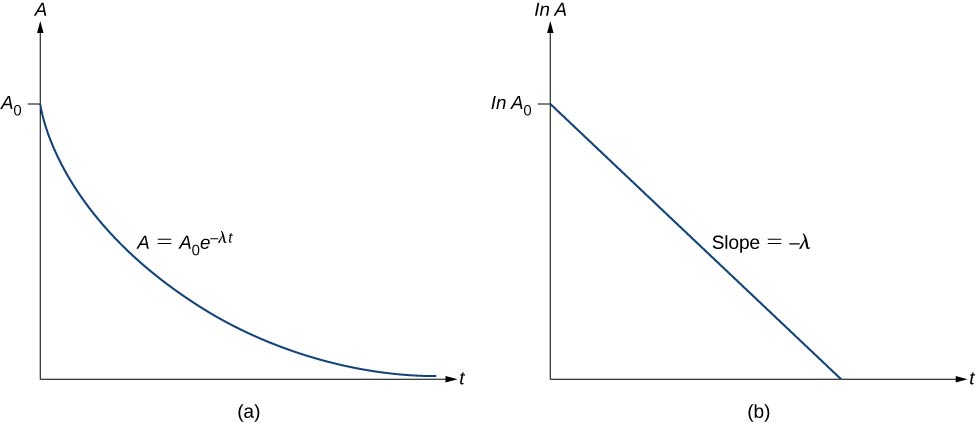
Decay Constant and Action of Strontium-90 The half-life of strontium-xc, ![]() , is 28.8 y. Find (a) its decay constant and (b) the initial activity of 1.00 g of the cloth.
, is 28.8 y. Find (a) its decay constant and (b) the initial activity of 1.00 g of the cloth.
Strategy We can detect the decay constant directly from (Figure). To determine the activity, nosotros first need to find the number of nuclei present.
Solution
- The decay constant is constitute to be
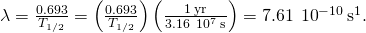
- The atomic mass of
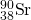 is 89.91 g. Using Avogadro's number
is 89.91 g. Using Avogadro's number 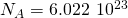 atoms/mol, we observe the initial number of nuclei in i.00 g of the textile:
atoms/mol, we observe the initial number of nuclei in i.00 g of the textile:
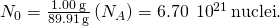
From this, nosotros find that the activity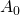 at
at 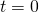 for 1.00 grand of strontium-90 is
for 1.00 grand of strontium-90 is
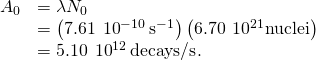
Expressing ![]() in terms of the half-life of the substance, we become
in terms of the half-life of the substance, we become
![]()
Therefore, the activity is halved subsequently one half-life. We can decide the disuse abiding ![]() past measuring the activity every bit a part of fourth dimension. Taking the natural logarithm of the left and correct sides of (Figure), nosotros get
past measuring the activity every bit a part of fourth dimension. Taking the natural logarithm of the left and correct sides of (Figure), nosotros get
![]()
This equation follows the linear form ![]() . If we plot ln A versus t, we wait a straight line with slope
. If we plot ln A versus t, we wait a straight line with slope ![]() and y-intercept
and y-intercept ![]() ((Figure)(b)). Activity A is expressed in units of becquerels (Bq), where i
((Figure)(b)). Activity A is expressed in units of becquerels (Bq), where i ![]() . This quantity tin can also exist expressed in decays per minute or decays per year. One of the most common units for action is the curie (Ci), defined to exist the activity of 1 chiliad of
. This quantity tin can also exist expressed in decays per minute or decays per year. One of the most common units for action is the curie (Ci), defined to exist the activity of 1 chiliad of ![]() . The relationship betwixt the Bq and Ci is
. The relationship betwixt the Bq and Ci is
![]()
What is ![]() Activity in Living Tissue? Approximately
Activity in Living Tissue? Approximately ![]() of the human trunk by mass is carbon. Summate the activity due to
of the human trunk by mass is carbon. Summate the activity due to ![]() in 1.00 kg of carbon institute in a living organism. Express the action in units of Bq and Ci.
in 1.00 kg of carbon institute in a living organism. Express the action in units of Bq and Ci.
Strategy The activity of ![]() is determined using the equation
is determined using the equation ![]() , where λ is the disuse abiding and
, where λ is the disuse abiding and ![]() is the number of radioactive nuclei. The number of
is the number of radioactive nuclei. The number of ![]() nuclei in a 1.00-kg sample is determined in two steps. Start, we decide the number of
nuclei in a 1.00-kg sample is determined in two steps. Start, we decide the number of ![]() nuclei using the concept of a mole. Second, we multiply this value by
nuclei using the concept of a mole. Second, we multiply this value by ![]() (the known abundance of
(the known abundance of ![]() in a carbon sample from a living organism) to determine the number of
in a carbon sample from a living organism) to determine the number of ![]() nuclei in a living organism. The decay constant is determined from the known half-life of
nuclei in a living organism. The decay constant is determined from the known half-life of ![]() (available from (Figure)).
(available from (Figure)).
Solution I mole of carbon has a mass of 12.0 g, since it is nearly pure ![]() . Thus, the number of carbon nuclei in a kilogram is
. Thus, the number of carbon nuclei in a kilogram is
![]()
The number of ![]() nuclei in 1 kg of carbon is therefore
nuclei in 1 kg of carbon is therefore
![]()
At present we tin can find the activity A by using the equation ![]() Entering known values gives u.s.
Entering known values gives u.s.
![]()
or ![]() decays per year. To convert this to the unit Bq, we but convert years to seconds. Thus,
decays per year. To convert this to the unit Bq, we but convert years to seconds. Thus,
![]()
or 250 decays per second. To limited A in curies, we use the definition of a curie,
![]()
Thus,
![]()
Significance Approximately ![]() of the human body by weight is carbon. Hundreds of
of the human body by weight is carbon. Hundreds of ![]() decays have place in the man body every 2nd. Carbon-14 and other naturally occurring radioactive substances in the torso compose a person'south background exposure to nuclear radiation. As we will see later in this chapter, this activity level is well below the maximum recommended dosages.
decays have place in the man body every 2nd. Carbon-14 and other naturally occurring radioactive substances in the torso compose a person'south background exposure to nuclear radiation. As we will see later in this chapter, this activity level is well below the maximum recommended dosages.
Radioactive Dating
Radioactive dating is a technique that uses naturally occurring radioactivity to decide the age of a material, such as a rock or an ancient antiquity. The basic approach is to estimate the original number of nuclei in a material and the nowadays number of nuclei in the material (after decay), and and so employ the known value of the decay constant ![]() and (Figure) to calculate the total time of the decay, t.
and (Figure) to calculate the total time of the decay, t.
An important method of radioactive dating is carbon-14 dating. Carbon-14 nuclei are produced when high-energy solar radiation strikes ![]() nuclei in the upper atmosphere and afterward decay with a half-life of 5730 years. Radioactive carbon has the aforementioned chemistry as stable carbon, and so it combines with the ecosphere and eventually becomes part of every living organism. Carbon-14 has an abundance of 1.iii parts per trillion of normal carbon. Therefore, if you know the number of carbon nuclei in an object, yous multiply that number by
nuclei in the upper atmosphere and afterward decay with a half-life of 5730 years. Radioactive carbon has the aforementioned chemistry as stable carbon, and so it combines with the ecosphere and eventually becomes part of every living organism. Carbon-14 has an abundance of 1.iii parts per trillion of normal carbon. Therefore, if you know the number of carbon nuclei in an object, yous multiply that number by ![]() to observe the number of
to observe the number of ![]() nuclei in that object. When an organism dies, carbon commutation with the environment ceases, and
nuclei in that object. When an organism dies, carbon commutation with the environment ceases, and ![]() is not replenished every bit it decays.
is not replenished every bit it decays.
By comparing the affluence of ![]() in an artifact, such as mummy wrappings, with the normal abundance in living tissue, it is possible to determine the mummy'south age (or the time since the person's death). Carbon-xiv dating tin be used for biological tissues as old as l,000 years, but is generally almost accurate for younger samples, since the abundance of
in an artifact, such as mummy wrappings, with the normal abundance in living tissue, it is possible to determine the mummy'south age (or the time since the person's death). Carbon-xiv dating tin be used for biological tissues as old as l,000 years, but is generally almost accurate for younger samples, since the abundance of ![]() nuclei in them is greater. Very old biological materials comprise no
nuclei in them is greater. Very old biological materials comprise no ![]() at all. The validity of carbon dating can be checked by other means, such as by historical knowledge or past tree-band counting.
at all. The validity of carbon dating can be checked by other means, such as by historical knowledge or past tree-band counting.
An Aboriginal Burial Cave In an aboriginal burial cave, your squad of archaeologists discovers ancient wood furniture. But ![]() of the original
of the original ![]() remains in the wood. How old is the furniture?
remains in the wood. How old is the furniture?
Strategy The problem statement implies that ![]() Therefore, the equation
Therefore, the equation ![]() can be used to find the product,
can be used to find the product, ![]() . We know the half-life of
. We know the half-life of ![]() is 5730 y, so we too know the decay abiding, and therefore the total decay fourth dimension t.
is 5730 y, so we too know the decay abiding, and therefore the total decay fourth dimension t.
Solution Solving the equation ![]() for
for ![]() gives us
gives us
![]()
Thus,
![]()
Taking the natural logarithm of both sides of the equation yields
![]()
so that
![]()
Rearranging the equation to isolate t gives the states
![]()
where
![]()
Combining this information yields
![]()
Significance The article of furniture is nearly 2000 years one-time—an impressive discovery. The typical uncertainty on carbon-14 dating is nearly 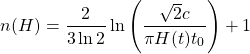 , and so the furniture is anywhere betwixt 1750 and 1950 years old. This date range must be confirmed by other testify, such equally historical records.
, and so the furniture is anywhere betwixt 1750 and 1950 years old. This date range must be confirmed by other testify, such equally historical records.
Check Your Understanding A radioactive nuclide has a high decay rate. What does this mean for its one-half-life and action?
Half-life is inversely related to disuse rate, so the half-life is curt. Activity depends on both the number of decaying particles and the disuse rate, so the action can be great or small.
Visit the Radioactive Dating Game to learn most the types of radiometric dating and effort your paw at dating some ancient objects.
Summary
Conceptual Questions
How is the initial action rate of a radioactive substance related to its half-life?
For the carbon dating described in this chapter, what important assumption is made about the time variation in the intensity of cosmic rays?
That it is constant.
Bug
A sample of radioactive material is obtained from a very quondam rock. A plot lnA verses t yields a gradient value of ![]() (encounter (Figure)(b)). What is the half-life of this fabric?
(encounter (Figure)(b)). What is the half-life of this fabric?
The decay constant is equal to the negative value of the gradient or ![]() The one-half-life of the nuclei, and thus the cloth, is
The one-half-life of the nuclei, and thus the cloth, is ![]()
Prove that: ![]() .
.
A sample of pure carbon-14 ![]() has an activeness of
has an activeness of ![]() What is the mass of the sample?
What is the mass of the sample?
A radioactive sample initially contains ![]() mol of a radioactive fabric whose half-life is 6.00 h. How many moles of the radioactive material remain after half-dozen.00 h? After 12.0 h? Subsequently 36.0 h?
mol of a radioactive fabric whose half-life is 6.00 h. How many moles of the radioactive material remain after half-dozen.00 h? After 12.0 h? Subsequently 36.0 h?
![]() ;
; ![]() ;
; ![]()
An former campfire is uncovered during an archaeological dig. Its charcoal is found to contain less than 1/grand the normal corporeality of ![]() . Estimate the minimum historic period of the charcoal, noting that
. Estimate the minimum historic period of the charcoal, noting that ![]()
Summate the activity ![]() , in curies of 1.00 g of
, in curies of 1.00 g of ![]() (b) Explain why your respond is not exactly 1.00 Ci, given that the curie was originally supposed to be exactly the activity of a gram of radium.
(b) Explain why your respond is not exactly 1.00 Ci, given that the curie was originally supposed to be exactly the activity of a gram of radium.
a. 0.988 Ci; b. The half-life of ![]() is more precisely known than information technology was when the Ci unit was established.
is more precisely known than information technology was when the Ci unit was established.
World War Ii aircraft had instruments with glowing radium-painted dials. The activity of i such instrument was ![]() Bq when new. (a) What mass of
Bq when new. (a) What mass of ![]() was nowadays? (b) Subsequently some years, the phosphors on the dials deteriorated chemically, but the radium did not escape. What is the activity of this musical instrument 57.0 years after information technology was made?
was nowadays? (b) Subsequently some years, the phosphors on the dials deteriorated chemically, but the radium did not escape. What is the activity of this musical instrument 57.0 years after information technology was made?
a. ![]() ; b.
; b. ![]()
The ![]() source used in a physics laboratory is labeled every bit having an activity of
source used in a physics laboratory is labeled every bit having an activity of ![]() on the date it was prepared. A pupil measures the radioactive decay of this source with a Geiger counter and observes 1500 counts per minute. She notices that the source was prepared 120 days before her lab. What fraction of the decays is she observing with her apparatus?
on the date it was prepared. A pupil measures the radioactive decay of this source with a Geiger counter and observes 1500 counts per minute. She notices that the source was prepared 120 days before her lab. What fraction of the decays is she observing with her apparatus?
Source: https://opentextbc.ca/universityphysicsv3openstax/chapter/radioactive-decay/
0 Response to "How to Read a Radioactive Decay Graph"
Post a Comment